代数-数学-知识点同步搜题

选择知识点

题型：

全部选择题填空题解答题

难易程度：

全部易较易中档较难难

题类筛选：

全部历年真题模拟题期末考试期中考试月考试卷单元测试其他

年份：

全部 2025 2024 2023 2022 2021 2020 更早

总题量：445选择本页全部试题

题型：解答题题类：期中考试难易度：较易
新
年份：2021

如图，四棱锥\(P-ABCD\)的底面为平行四边形．设平面\(PAD\)与平面\(PBC\)的交线为\(l\)，\(M\)、\(N\)、\(Q\)分别为\(PC\)、\(CD\)、\(AB\)的中点．
\((1)\)求证：平面\(MNQ/\!/\)平面\(PAD\)；
\((2)\)求证：\(BC/\!/l.\)

查看解析收藏纠错

+选题
题型：选择题题类：期末考试难易度：较易
新测
年份：2021

设\(m\)，\(n\)是两条不同的直线，\(α\)，\(β\)是两个不同的平面，则下列命题正确的是\((\quad)\)

A.若\(α⊥β\)，\(m⊂α\)，\(n⊂β\)，则\(m⊥n\) B.若\(m⊥α\)，\(m⊂β\)，则\(α⊥β\) C.若\(m/\!/α\)，\(n/\!/α\)，则\(m/\!/n\) D.若\(m/\!/α\)，\(m/\!/β\)，则\(α/\!/β\)

查看解析收藏纠错

+选题
题型：解答题题类：期末考试难易度：较易
新
年份：2021

如图，\(ABB_{1}A_{1}\)为圆柱\(OO_{1}\)的轴截面\((\)即过旋转轴的截面\()\)，\(CC_{1}\)为其一条母线\((\)不与\(AA_{1}\)，\(BB_{1}\)重合\().\)
\((1)\)求证：平面\(AA_{1}C_{1}C⊥\)平面\(BB_{1}C_{1}C\)；
\((2)\)求证：平面\(AO_{1}C_{1}/\!/\)平面\(B_{1}OC.\)

查看解析收藏纠错

+选题
题型：填空题题类：月考试卷难易度：较易
新
年份：2021

在正四棱柱\(ABCD-A_{1}B_{1}C_{1}D_{1}\)中，\(O\)为底面\(ABCD\)的中心，\(P\)是\(DD_{1}\)的中点，设\(Q\)是\(CC_{1}\)上的点，则点\(Q\)满足条件 ______时，有平面\(D_{1}BQ/\!/\)平面\(PAO.\)

查看解析收藏纠错

+选题
题型：解答题题类：期中考试难易度：较易
新
年份：2021

如图，在直四棱柱\(ABCD-A_{1}B_{1}C_{1}D_{1}\)中，底面\(ABCD\)为正方形，\(AA_{1}=2AB=4\)，\(M\)，\(N\)，\(P\)分别是\(AD\)，\(DD_{1}\)，\(CC_{1}\)的中点．
\((1)\)证明：平面\(MNC/\!/\)平面\(AD_{1}P\)；
\((2)\)求三棱锥\(D_{1}-ADP\)的体积．

查看解析收藏纠错

+选题
题型：选择题题类：期中考试难易度：较易
新测
年份：2021

已知\(l\)，\(m\)是空间中两条不同的直线，\(α\)，\(β\)是空间中两个不同的平面，下列说法正确的是
\((\quad)\)

A.若\(l⊥α\)，\(m\://\:l\)，\(m⊂β\)，则\(α⊥β\) B.若\(α\://\:β\)，\(l\://\:α\)，则\(l\://\:β\) C.若\(l⊥m\)，\(l⊥α\)， \(α\://\:β\)，则\(m\://\:β\) D.若\(α⊥β\)，\(l\://\:α\)，则\(l⊥β\)

查看解析收藏纠错

+选题
题型：解答题题类：期中考试难易度：较易
新
年份：2021

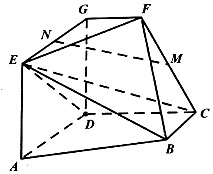
如图，\(AD/\!/BC\)且\(AD=2BC\)，\(AD⊥CD\)，\(EG/\!/AD\)且\(EG=AD\)，\(CD/\!/FG\)且\(CD=2FG\)，\(DG⊥\)平面\(ABCD\)，\(DA=DC=DG=2.\)
\((1)\)若点\(M\)为\(CF\)的中点，点\(N\)为\(EG\)的中点，点\(P\)为线段\(DG\)上动点，且平面\(MNP/\!/\)平面\(CDE\)，求\(\dfrac{GP}{GD}\)的值；
\((2)\)求二面角\(E-BC-F\)的正弦值．

查看解析收藏纠错

+选题
题型：解答题题类：月考试卷难易度：较易
新
年份：2021

\((1)\)如图\(1\)，空间四边形\(ABCD\)中，\(E\)、\(H\)分别是\(AB\)、\(AD\)的中点，\(F\)、\(G\)分别是\(BC\)、\(CD\)上的点，且\(\dfrac{CF}{CB}=\dfrac{CG}{CD}=\dfrac{3}{4}.\)求证：直线\(EF\)与\(GH\)的交点在直线\(AC\)上．

\((2)\)如图\(2\)，\(α/\!/β\)，点\(P\)是平面\(α\)、\(β\)外一点，从点\(P\)引三条不共面的射线\(PA\)、\(PB\)、\(PC\)，与平面\(α\)分别相交于点\(A\)、\(B\)、\(C\)，与平面\(β\)分别相交于\(A’\)、\(B’\)、\(C’\)，求证：\(\triangle ABC\)∽\(\triangle A'B'C'.\)

查看解析收藏纠错

+选题
题型：解答题题类：期末考试难易度：较易
新
年份：2021

如图，四边形\(ABCD\)是矩形，\(ED⊥\)平面\(ABCD\)，\(FB⊥\)平面\(ABCD\)，\(BC=3\)，\(DE=CD=2FB=2.\)
\((1)\)证明：平面\(AED/\!/\)平面\(BCF.\)
\((2)\)求三棱锥\(B-CEF\)的体积．

查看解析收藏纠错

+选题
题型：解答题题类：期末考试难易度：较易
新
年份：2021

如图所示，在四棱锥\(P-ABCD\)中，底面\(ABCD\)是直角梯形，\(AD/\!/BC\)，\(∠BCD=90°\)，\(E\)，\(F\)分别是棱\(BC\)，\(PC\)的中点，且\(AD=CD=\dfrac{1}{2}BC=\sqrt{2}.\)
\((1)\)求证：平面\(PAB/\!/\)平面\(FED\)；
\((2)\)若点\(P\)在平面\(ABCD\)内的射影\(H\)恰为\(AB\)的中点，设\(PH=1\)，求二面角\(C-EF-D\)的余弦值．

查看解析收藏纠错

+选题

高中

选择知识点

服务介绍

帮助中心