题型:填空题 题类:其他 难易度:较难
年份:2018
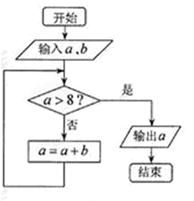
\((1)\)执行如图所示的程序框图,如果输入\(a=1,b=2\),则输出的\(a\)的值为_____ .
\((2).\)将函数\(y=\sin 2x \)的图象向左平移\( \dfrac{π}{4} \)个单位,再将图象上各点的横坐标伸长到原来的\(2\)倍,纵坐标不变,则所得图象对应的函数解析式是_____________\((\)结论写成最简形式\()\).
\((3).\)函数\(y=\sqrt{\tan \left( \dfrac{x}{2}-\dfrac{\pi }{6} \right)-\sqrt{3}}\)有意义的\(x\)的集合为__________________________________ .
\((4).\)已知函数\(f(x)=\begin{cases}\cos \left(- \dfrac{3π}{2}+πx\right)x\leqslant 0 \\ \dfrac{1}{ \sqrt[3]{2}}f(x-1),x > 0\end{cases} \),\(g(x)=\ln \left| \dfrac{3x}{5} \right|\),则函数\(f(x)-g(x)\)的零点有_______个.
题型:填空题 题类:其他 难易度:中档
年份:2018
\((1)\sqrt{{{(\pi -4)}^{2}}}+{{\log }_{2}}({{4}^{7}}\times {{2}^{5}})-\pi \ln \dfrac{1}{e}=\)_________.
\((2)\)函数\(f(x)=\dfrac{\lg (2-x)}{\sqrt{x+1}}\)的定义域是_______.
\((3)\)命题“\(\exists x\in R\),\({{x}^{2}}-(m-1)x+1 < 0\)”为假命题,则实数\(m\)的取值范围为_________.
\((4)\)已知函数\(f\left(x\right)= \dfrac{\ln x}{x} \),\(g\left(x\right)=-e{x}^{2}+ax (e\)是自然对数的底数\()\),对任意的\({x}_{1}∈R R\),存在\({x}_{2}∈\left[ \dfrac{1}{3},2\right] \),有\(f(x_{1})\leqslant g(x_{2})\),则\(a\)的取值范围为___________.