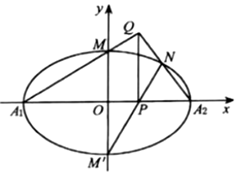已知椭圆\(C\)：\( \dfrac {x^{2}}{a^{2}}+ \dfrac {y^{2}}{b^{2}}=1(a > b > 0)\)的离心率\(e= \dfrac { \sqrt {6}}{3}\)，短轴长为\(2\)，\(M\)、\(M{'}\)是椭圆\(C\)上、下两个顶点，\(N\)在椭圆\(C\)上且非顶点，直线\(M{'}N\)交\(x\)轴于点\(P\)，\(A _{1}\)，\(A _{2}\)是椭圆\(C\)的左，右顶点，直线\(A _{1} M\)，\(A _{2} N\)交于点\(Q\)．
\((1)\)求椭圆\(C\)的方程；
\((2)\)证明：直线\(PQ\)与\(y\)轴平行．